Torus Obstructions

A torus is the orientable surface that has one handle. Here is a picture of a graph embedded on the torus:

The two green arcs should be identified to make a cylinder, then identify the red arcs to make the torus. A graph G is a topological obstruction for the torus if G has minimum degree at least three, and G does not embed on the torus but for all edges e in G, G-e embeds on the torus. A graph G is a minor order obstruction for the torus if G is a topological obstruction for the torus and for all edges e in G, G contract e embeds on the torus. A torus obstruction G is split-delete minimal if G cannot be obtained from an obstruction that has one less vertex by splitting at some vertex and then deleting some subset of the edges.

This page contains all of the torus obstructions that we have discovered so far. This work is explained in the paper:

The input format for the torus obstructions is upper triangular adjacency format. Each graph starts with the number of vertices and this is followed by the upper triangle of the adjacency matrix (not including the diagonal elements). Here is an example of a graph and its upper triangular adjacency matrix input format:

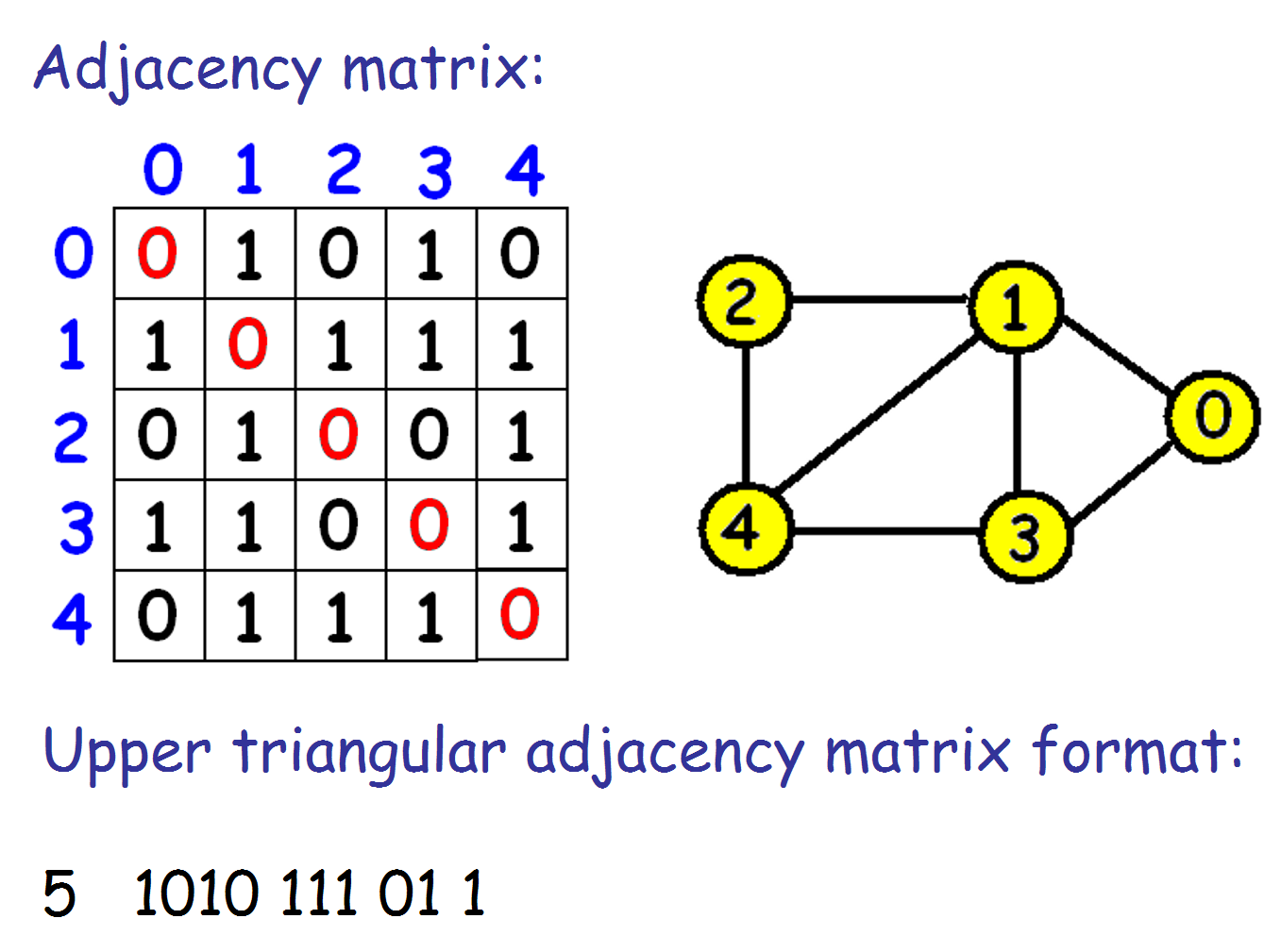
There has to be a space after the number of vertices, but other spaces are optional. The files given here have one graph per line and no spaces. For example, the above graph is recorded like this: 

5 1010111011

The obstructions:

  1. All obstructions known so far:
    all_obs.txt or the compressed file all_obs.txt.gz
  2. All minor order obstructions known so far:
    all_minor_obs.txt or the compressed file all_minor_obs.txt.gz
  3. All split-delete minimal obstructions known so far.
    all_sd_minimal_obs.txt or the compressed file all_sd_minimal_obs.txt.gz

The numbers of vertices and edges in these obstructions are:

For all of the obstructions: 

# Edges      : 18 19 20  21  22   23    24    25    26    27   28   29   30  31  32 33 34 35 36 
   8 Vertices:  0  0  0   0   1    0     1     1     0     0    0    0    0   0   0  0  0  0  0 
   9 Vertices:  0  2  5   2   9   17     6     2     5     0    0    0    0   0   0  0  0  0  0 
  10 Vertices:  0 15  9  35  40  190   170   102    76    21    1    0    1   0   0  0  0  0  0 
  11 Vertices:  5  2 49  87 270  892  1878  1092   501   125   22    4    1   0   0  0  0  0  0 
  12 Vertices:  1 12  6 201 808 2698  6690  6387  1971   499   98   10    3   1   0  0  0  0  0 
  13 Vertices:  0  0 12  19 820 4967 12781 16727  7287  1548  301   63    7   0   0  0  0  0  0 
  14 Vertices:  0  0  0   9  38 2476 15219 24355 16397  4053  930  259   32   1   0  0  0  0  0 
  15 Vertices:  0  0  0   0   0   33  3646 22402 20957  8474 1948  812  197  10   0  0  0  0  0 
  16 Vertices:  0  0  0   0   0    0    20  2689 17469 10582 3150 1317  777  68   2  0  0  0  0 
  17 Vertices:  0  0  0   0   0    0     0     0   837  8099 4154 1131 1073 434  11  0  0  0  0 
  18 Vertices:  0  0  0   0   0    0     0     0     0   133 2332 1472  526 642 156  1  0  0  0 
  19 Vertices:  0  0  0   0   0    0     0     0     0     0    0  393  435 294 256 48  0  0  0 
  20 Vertices:  0  0  0   0   0    0     0     0     0     0    0    0   39 100 164 63 17  0  0 
  21 Vertices:  0  0  0   0   0    0     0     0     0     0    0    0    0   0  16 63 12  4  0 
  22 Vertices:  0  0  0   0   0    0     0     0     0     0    0    0    0   0   0  2 22  1  1 
  23 Vertices:  0  0  0   0   0    0     0     0     0     0    0    0    0   0   0  0  0  4  0 
  24 Vertices:  0  0  0   0   0    0     0     0     0     0    0    0    0   0   0  0  0  0  2 

  8 Vertices:       3
  9 Vertices:      48
 10 Vertices:     660
 11 Vertices:    4928
 12 Vertices:   19385
 13 Vertices:   44532
 14 Vertices:   63769
 15 Vertices:   58479
 16 Vertices:   36074
 17 Vertices:   15739
 18 Vertices:    5262
 19 Vertices:    1426
 20 Vertices:     383
 21 Vertices:      95
 22 Vertices:      26
 23 Vertices:       4
 24 Vertices:       2
Number of graphs:     250815

For the minor order obstructions: 

# Edges      : 18 19 20 21  22   23   24   25  26 27 28 29 30 31 
   8 Vertices:  0  0  0  0   1    0    1    1   0  0  0  0  0  0 
   9 Vertices:  0  2  5  2   9   13    6    2   4  0  0  0  0  0 
  10 Vertices:  0 15  3 18  31  117   90   92  72 17  1  0  1  0 
  11 Vertices:  5  2  0 46 131  569  998  745 287 45  8  3  1  0 
  12 Vertices:  1  0  0 52 238 1218 2519 1841 505 91 23  2  1  1 
  13 Vertices:  0  0  0  5  98  836 1985 1924 512 84 46  2  1  0 
  14 Vertices:  0  0  0  0   9   68  463  943 251 43 86  1  0  0 
  15 Vertices:  0  0  0  0   0    0   21  118  45 12 85  0  0  0 
  16 Vertices:  0  0  0  0   0    0    0    4   3  5 41  0  0  0 
  17 Vertices:  0  0  0  0   0    0    0    0   0  0  8  0  0  0 
  18 Vertices:  0  0  0  0   0    0    0    0   0  0  1  0  0  0 

  8 Vertices:       3
  9 Vertices:      43
 10 Vertices:     457
 11 Vertices:    2840
 12 Vertices:    6492
 13 Vertices:    5493
 14 Vertices:    1864
 15 Vertices:     281
 16 Vertices:      53
 17 Vertices:       8
 18 Vertices:       1
Number of graphs:      17535

For the split-delete minimal obstructions: 

# Edges      : 20 21 22 23 24 25 26 27 28 29 30 31 
   8 Vertices:  0  0  1  0  1  1  0  0  0  0  0  0 
   9 Vertices:  2  0  2  3  3  1  4  0  0  0  0  0 
  10 Vertices:  0  1  0  1 16 40 54 17  1  0  1  0 
  11 Vertices:  0  0  0  0  4 44 36 15  7  3  1  0 
  12 Vertices:  0  0  0  0  2 31 41 17  3  1  1  1 
  13 Vertices:  0  0  0  0  2  6 24  5  3  0  0  0 
  14 Vertices:  0  0  0  0  0  2  4  0  0  0  0  0 

  8 Vertices:       3
  9 Vertices:      15
 10 Vertices:     131
 11 Vertices:     110
 12 Vertices:      97
 13 Vertices:      40
 14 Vertices:       6
Number of graphs:        402

This repository of obstructions is also available at https://webhome.cs.uvic.ca/~wendym/torus/torus_obstructions.html which, along with this site, will also be updated if any significant progress is made. If you find any more torus obstructions, please send them to Wendy Myrvold (wendym@uvic.ca) in upper triangular adjacency format so that they can be added to the database.