| |
|
Abstract: |
Mixed arithmetic and geometric means, with and without weights, are both considered. Related to mixed arithmetic and geometric means, the following three types of inequalities and their generalizations, from three variables to a general 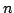 variables, are studied. For arbitrary variables, are studied. For arbitrary 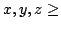 0 we have 0 we have
The main results include generalizations of J.C. Burkill's inequalities (J.C. Burkill; The concavity of discrepancies in inequalities of means and of Hölder, J. London Math. Soc. (2), 7 (1974), 617-626), and a positive solution for the conjecture considered by B.C. Carlson, R.K. Meany and S.A. Nelson (B.C. Carlson, R.K. Meany, S.A. Nelson; Mixed arithmetic and geometric means, Pacific J. of Math., 38 (1971), 343-347).
|



