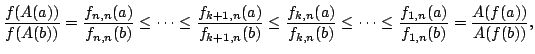JIPAM
| Inequalities of Jensen-Pečaric-Svrtan-Fan Type | ||||||
| Authors: | Chaobang Gao, Jiajin Wen, | |||||
| Keywords: | Jensen's inequality, Pe{c}ari'c-Svrtan's inequality, Fan's inequality, Theory of majorization, Hermite matrix. | |||||
| Date Received: | 22/01/07 | |||||
| Date Accepted: | 06/07/08 | |||||
| Subject Codes: |
26D15, 26E60. |
|||||
| Editors: | Sever S. Dragomir, | |||||
| Abstract: |
By using the theory of majorization, the following inequalities of Jensen-Pecaric-Svrtan-Fan type are established: Let
the inequalities are reversed for
http://jipam.vu.edu.au The URL for this article is: http://jipam.vu.edu.au/article.php?sid=1011 | |||||