JIPAM

A Multinomial Extension of an Inequality of Haber  
 
  Authors: Hacčne Belbachir,  
  Keywords: Haber inequality, multinomial coefficient, symmetric functions.  
  Date Received: 10/07/08  
  Date Accepted: 17/09/08  
  Subject Codes:

05A20, 05E05.

  
  Editors: László Tóth,  
 
  Abstract:

In this paper, we establish the following: Let 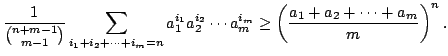$ a_{1},a_{2},ldots ,a_{m}$ be non negative real numbers, then for all $ ngeq 0,$ we have

$displaystyle frac{1}{inom{n+m-1}{m-1}}sum_{i_{1}+i_{2}+cdots +i_{m}=n}a_{... ...cdots a_{m}^{i_{m}}geq left( frac{a_{1}+a_{2}+cdots +a_{m}}{m}ight)^{n}.$
The case $ m=2$ gives the Haber inequality. We apply the result to find lower bounds for the sum of reciprocals of multinomial coefficients and for symmetric functions. ;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=1040