| |
|
|
| |
Volume 10, Issue 1, Article 2 |
|
|
|
|
|
| |
A Spanning Set for the Space of Super Cusp Forms
|
| |
|
Authors: |
Roland Knevel, |
|
| |
|
Keywords:
|
Automorphic and cusp forms, super symmetry, semisimple Lie groups, partially hyperbolic flows, unbounded realization of a complex bounded symmetric domain. |
|
| |
|
Date Received:
|
18/07/08 |
|
| |
|
Date Accepted:
|
09/02/09 |
|
| |
|
Subject Codes: |
Pri: 11F55; Sec: 32C11
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
The aim of this article is the construction of a spanning set for the space 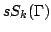 of super cusp forms on a complex bounded symmetric super domain of super cusp forms on a complex bounded symmetric super domain 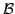 of rank of rank 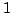 with respect to a lattice with respect to a lattice 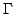 . The main ingredients are a generalization of the ANOSOV closing lemma for partially hyperbolic diffeomorphisms and an unbounded realization . The main ingredients are a generalization of the ANOSOV closing lemma for partially hyperbolic diffeomorphisms and an unbounded realization 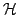 of of 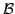 , in particular FOURIER decomposition at the cusps of the quotient , in particular FOURIER decomposition at the cusps of the quotient 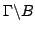 mapped to mapped to  via a partial CAYLEY transformation. The elements of the spanning set are in finite-to-one correspondence with closed geodesics of the body via a partial CAYLEY transformation. The elements of the spanning set are in finite-to-one correspondence with closed geodesics of the body 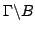 of of 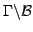 , the number of elements corresponding to a geodesic growing linearly with its length. , the number of elements corresponding to a geodesic growing linearly with its length.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



