| |
|
|
| |
Volume 10, Issue 1, Article 18 |
|
|
|
|
|
| |
Approximation, Numerical Differentiation and Integration Based on Taylor Polynomial
|
| |
|
Authors: |
Gancho Tachev, |
|
| |
|
Keywords:
|
Degree of approximation, Taylor polynomial, $P_n$-simple functionals, least concave majorant of $omega(f,cdot)$. |
|
| |
|
Date Received:
|
13/11/08 |
|
| |
|
Date Accepted:
|
09/02/09 |
|
| |
|
Subject Codes: |
41A05, 41A15, 41A25, 41A55, 41A58, 65D05
|
|
| |
|
Editors: |
Ioan Gavrea, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
We represent new estimates of errors of quadrature formula, formula of numerical differentiation and approximation using Taylor polynomial. To measure the errors we apply representation of the remainder in Taylor formula by least concave majorant of the modulus of continuity of the 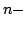 th derivative of an th derivative of an 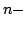 times differentiable function. Our quantitative estimates are special applications of a more general inequality for times differentiable function. Our quantitative estimates are special applications of a more general inequality for 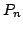 -simple functionals. -simple functionals.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



