| |
|
|
| |
Volume 10, Issue 1, Article 23 |
|
|
|
|
|
| |
Integral Mean Estimates for Polynomials whose Zeros are within a Circle
|
| |
|
Authors: |
K. K. Dewan, Naresh Singh, Barchand Chanam, Abdullah Mir, |
|
| |
|
Keywords:
|
Polynomials, Zeros of order $m$, Inequalities, Polar derivatives. |
|
| |
|
Date Received:
|
17/10/07 |
|
| |
|
Date Accepted:
|
19/12/08 |
|
| |
|
Subject Codes: |
30A10, 30C10, 30D15
|
|
| |
|
Editors: |
Gradimir V. Milovanovic, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let  be a polynomial of degree be a polynomial of degree 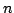 . Zygmund [11] has shown that for . Zygmund [11] has shown that for 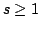 In this paper, we have obtained inequalities in the reverse direction for the polynomials having a zero of order  at the origin. We also consider a problem for the class of polynomials at the origin. We also consider a problem for the class of polynomials 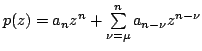 not vanishing outside the disk not vanishing outside the disk 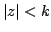 , ,  and obtain a result which, besides yielding some interesting results as corollaries, includes a result due to Aziz and Shah [Indian J. Pure Appl. Math., 28 (1997), 1413-1419] as a special case. and obtain a result which, besides yielding some interesting results as corollaries, includes a result due to Aziz and Shah [Indian J. Pure Appl. Math., 28 (1997), 1413-1419] as a special case.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



