| |
|
|
| |
Volume 10, Issue 2, Article 33 |
|
|
|
|
|
| |
On a Weighted Interpolation of Functions with Circular Majorant
|
| |
|
Authors: |
Simon J. Smith, |
|
| |
|
Keywords:
|
Interpolation, Lagrange interpolation, Weighted interpolation, Circular majorant, Projection norm, Lebesgue constant, Chebyshev polynomial. |
|
| |
|
Date Received:
|
31/07/08 |
|
| |
|
Date Accepted:
|
06/02/09 |
|
| |
|
Subject Codes: |
41A05, 41A10.
|
|
| |
|
Editors: |
Qazi Ibadur Rahman, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Denote by 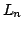 the projection operator obtained by applying the Lagrange interpolation method, weighted by the projection operator obtained by applying the Lagrange interpolation method, weighted by 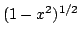 , at the zeros of the Chebyshev polynomial of the second kind of degree , at the zeros of the Chebyshev polynomial of the second kind of degree 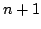 . The norm . The norm 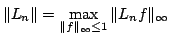 , where , where 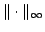 denotes the supremum norm on denotes the supremum norm on  , is known to be asymptotically the same as the minimum possible norm over all choices of interpolation nodes for unweighted Lagrange interpolation. Because the projection forces the interpolating function to vanish at , is known to be asymptotically the same as the minimum possible norm over all choices of interpolation nodes for unweighted Lagrange interpolation. Because the projection forces the interpolating function to vanish at 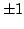 , it is appropriate to consider a modified projection norm , it is appropriate to consider a modified projection norm 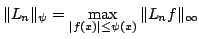 , where , where  is a given function (a curved majorant) that satisfies is a given function (a curved majorant) that satisfies 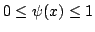 and and 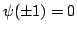 . In this paper the asymptotic behaviour of the modified projection norm is studied in the case when . In this paper the asymptotic behaviour of the modified projection norm is studied in the case when  is the circular majorant is the circular majorant 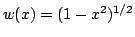 . In particular, it is shown that asymptotically . In particular, it is shown that asymptotically 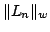 is smaller than is smaller than  by the quantity by the quantity 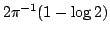 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



