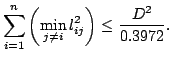JIPAM

On the Interpoint Distance Sum Inequality  
 
  Authors: Yong Xia, Hong-Ying Liu,  
  Keywords: Combinatorial geometry, Distance geometry, Interpoint distance sum inequality, Optimization.  
  Date Received: 10/04/2009  
  Date Accepted: 28/09/2009  
  Subject Codes:

51D20, 51K05, 52C26.

  
  Editors: Peter S. Bullen,  
 
  Abstract:

Let $ n$ points be arbitrarily placed in $ B(D)$, a disk in $ mathbb{R}^2$ having diameter $ D$. Denote by $ l_{ij}$ the Euclidean distance between point $ i$ and $ j$. In this paper, we show

$displaystyle sum_{i=1}^n left(min_{j<br />eq i}l_{ij}^2ight) leq frac{D^2}{0.3972}.$    
We then extend the result to $ mathbb{R}^3$. ;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=1130