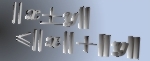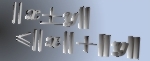| |
|
Abstract: |
Let 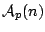 be the class of analytic and multivalent functions be the class of analytic and multivalent functions 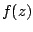 in the open unit disk in the open unit disk 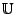 . Furthermore, let . Furthermore, let 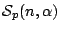 and and 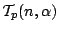 be the subclasses of be the subclasses of 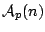 consisting of multivalent starlike functions consisting of multivalent starlike functions 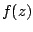 of order of order 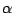 and multivalent convex functions and multivalent convex functions 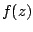 of order of order 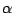 , respectively. Using the coefficient inequalities for , respectively. Using the coefficient inequalities for 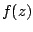 to be in to be in 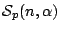 and and 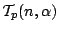 , new subclasses , new subclasses 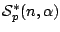 and and 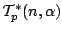 are introduced. Applying the Hölder inequality, some interesting properties of generalizations of convolutions (or Hadamard products) for functions are introduced. Applying the Hölder inequality, some interesting properties of generalizations of convolutions (or Hadamard products) for functions 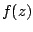 in the classes in the classes 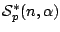 and and 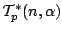 are considered. are considered.
|