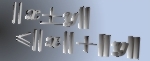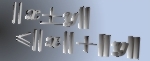| |
|
Abstract: |
For subharmonic functions 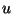 in in 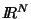 , of Riesz measure , of Riesz measure 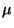 , the growth of the function , the growth of the function 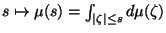 ( (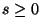 ) is described and compared with the growth of ) is described and compared with the growth of 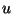 . It is also shown that, if . It is also shown that, if ![$ int_{{ I!! R}^N} u^+ (x) [-varphi ' (vert xvert ^2)] dx <+infty$](images/030_00_JIPAM/img6.gif) for some decreasing for some decreasing 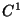 function function 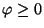 , then , then 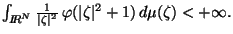 Given two subharmonic functions Given two subharmonic functions 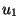 and and 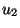 , of Riesz measures , of Riesz measures 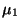 and and 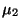 , with a growth like , with a growth like 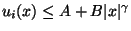 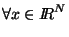 ( (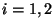 ), it is proved that ), it is proved that 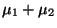 is not necessarily the Riesz measure of any subharmonic function is not necessarily the Riesz measure of any subharmonic function 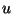 with such a growth as with such a growth as 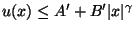 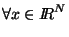 (here (here 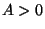 , , 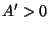 and and 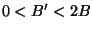 ). ).
|