| |
|
Abstract: |
It is well-known that inequalities between means play a very important role in many branches of mathematics. Please refer to [1,3,7], etc. The main aims of the present article are:
(i)
- to show that there are monotonic and continuous functions
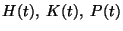 and and 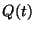 on on ![$ left[ 0,1right] $](images/035_00_JIPAM/img3.gif) such that for all such that for all ![$ tin lbrack 0,1],$](images/035_00_JIPAM/img4.gif) and
and where 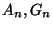 and and 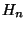 are respectively the weighted arithmetic, geometric and harmonic means of the positive numbers are respectively the weighted arithmetic, geometric and harmonic means of the positive numbers 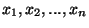 in in ![$(0,1/2],$](images/035_00_JIPAM/img10.gif) with positive weights with positive weights 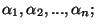 while while 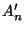 and and 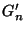 are respectively the weighted arithmetic and geometric means of the numbers are respectively the weighted arithmetic and geometric means of the numbers 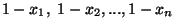 with the same positive weights with the same positive weights 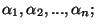
(ii)
- to present more general monotonic refinements for the Ky Fan
inequality as well as some inequalities involving means; and
(iii)
- to present some generalized and new inequalities in this connection.
[1] H. ALZER, Inequalities for arithmetic, geometric and harmonic means, Bull. London Math. Soc., 22 (1990), 362–366.
[3] P.S. BULLEN, D.S. MITRINOVIC and J.E. PECARIC, Means and Their Inequalities, Reiddel Dordrecht, 1988.
[7] A.M. FINK, J.E. PECARIC and D.S. MITRINOVIC, Classical and New Inequalities in Analysis , Kluwer Academic
Publishers, 1993.
|



