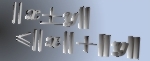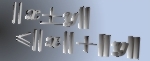| |
|
|
| |
Volume 2, Issue 3, Article 27 |
|
|
|
|
|
| |
Generalized Auxiliary Problem Principle and Solvability of a Class of Nonlinear Variational Inequalities Involving Cocoercive and Co-Lipschitzian Mappings
|
| |
|
Authors: |
Ram U. Verma, |
|
| |
|
Keywords:
|
Generalized auxiliary variational inequality problem, Cocoercive mappings, Approximation-solvability, Approximate solutions, Partially relaxed monotone mappings. |
|
| |
|
Date Received:
|
31/12/00 |
|
| |
|
Date Accepted:
|
15/03/01 |
|
| |
|
Subject Codes: |
49J40
|
|
| |
|
Editors: |
Drumi Bainov, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
The approximation-solvability of the following class of nonlinear variational inequality (NVI) problems, based on a new generalized auxiliary problem principle, is discussed.
Find an element 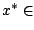 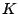 such that such that 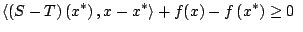 for all 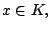 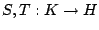 are mappings from a nonempty closed convex subset are mappings from a nonempty closed convex subset 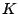 of a real Hilbert space of a real Hilbert space 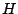 into into 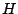 , and , and 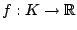 is a continuous convex functional on is a continuous convex functional on 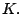 The generalized auxiliary problem principle is described as follows: for given iterate The generalized auxiliary problem principle is described as follows: for given iterate 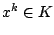 and, for constants and, for constants 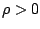 and and 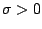 ), find ), find 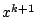 such that such that
where
where 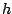 is a functional on is a functional on 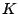 and and 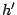 the derivative of the derivative of 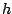 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|