26D15,41A55.

Integral inequalities of Ostrowski type are developed for 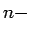times differentiable mappings, with multiple branches, on the 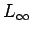norm. Some particular inequalities are also investigated, which include explicit bounds for perturbed trapezoid, midpoint, Simpson's, Newton-Cotes and left and right rectangle rules. The results obtained provide sharper bounds than those obtained by Dragomir [5] and Cerone, Dragomir and Roumeliotis [2].

[2] P. CERONE, S.S. DRAGOMIR and J. ROUMELIOTIS, An inequality of Ostrowski type for mappings whose second derivatives are bounded and applications, East Asian J. of Math., 15(1) (1999), 1-9.
[5]  S.S. DRAGOMIR, A generalization of Ostrowski's integral inequality for mappings whose derivatives belong to 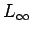[a, b] and applications in numerical integration, SUT. J. of Math., (in press)