| |
|
|
| |
Volume 3, Issue 3, Article 43 |
|
|
|
|
|
| |
Inequalities on Linear Functions and Circular Powers
|
| |
|
Authors: |
Pantelimon Stanica, |
|
| |
|
Keywords:
|
Binary Sequences, Fibonacci Numbers, Linear Forms, Inequalities. |
|
| |
|
Date Received:
|
25/02/02 |
|
| |
|
Date Accepted:
|
10/04/02 |
|
| |
|
Subject Codes: |
11B37,11B39,26D15.
|
|
| |
|
Editors: |
Constantin P. Niculescu, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
We prove some inequalities such as where  is a linear function or a linear function in logarithms and is a linear function or a linear function in logarithms and 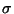 is a permutation, which is a product of disjoint translation cycles. Stronger inequalities are proved for second-order recurrence sequences, generalizing those of Diaz. is a permutation, which is a product of disjoint translation cycles. Stronger inequalities are proved for second-order recurrence sequences, generalizing those of Diaz.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



