|
For the given arbitrary sequence of real numbers 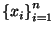 we construct several lower and upper bound converging sequences. Our goal is to localize the absolute value of the sequence maximum. Also we could calculate the quantity of such numbers. Since the proposed algorithms are iterative, asymptotical convergence theorems are proved.
The presented task seems to be senseless from the ordinary point of view, but we illustrate its importance for a set of applied problems: matrix analysis, measurement data processing; Monte Carlo methods. According to the modern conception of fault tolerant computations, also known as ''interval analysis``, these results could be treated as a part of interval mathematics too.
| 
Home
