26A42,41A55

We give error bounds for the trapezoidal rule and Simpson's rule for ``rough'' continuous functions--for instance, functions which are Hölder continuous, of bounded variation, or which are absolutely continuous and whose derivative is in 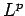. These differ considerably from the classical results, which require the functions to have continuous higher derivatives. Further, we show that our results are sharp, and in many cases precisely characterize the functions for which equality holds. One consequence of these results is that for rough functions, the error estimates for the trapezoidal rule are better (that is, have smaller constants) than those for Simpson's rule.