JIPAM
| On Some Inequalities of Local Times of Iterated Stochastic Integrals | ||||
| Authors: | Litan Yan, | |||
| Keywords: | Continuous local martingale, Continuous semimartingale, Iterated stochastic integrals, Local time, Random time, Burkholder-Davis-Gundy inequalities, Barlow-Yor inequalities. | |||
| Date Received: | 06/07/01 | |||
| Date Accepted: | 25/06/02 | |||
| Subject Codes: |
60H05,60G44,60J55. |
|||
| Editors: | Neil S. Barnett, | |||
| Abstract: |
Let 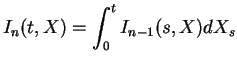 | |||
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=214