| |
|
Abstract: |
In this paper, it is shown that if 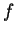 is a non-constant entire function, is a non-constant entire function, 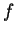 and and 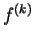 share the small function share the small function 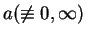 CM and CM and 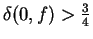 , then , then 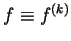 . Furthermore, if . Furthermore, if 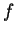 is non-constant meromorphic, is non-constant meromorphic, 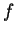 and and 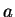 do not have any common pole and do not have any common pole and 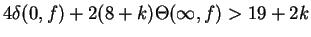 , then the same conclusion can be obtained. Finally, some open questions are posed for the reader. , then the same conclusion can be obtained. Finally, some open questions are posed for the reader.
|



