| |
|
Abstract: |
In [2] the second author proposed to find a description (or examples) of real-valued 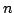 -variable functions satisfying the following two inequalities: -variable functions satisfying the following two inequalities: if 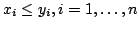 , then , then 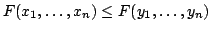 , , | | with strict inequality if there is an index 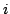 such that such that 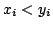 ; and for ; and for 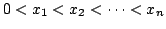 , then, In this short note we extend in a direction a result of [2] and we prove a theorem that provides a large class of examples satisfying the two inequalities, with , then, In this short note we extend in a direction a result of [2] and we prove a theorem that provides a large class of examples satisfying the two inequalities, with 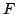 replaced by any symmetric polynomial with positive coefficients. Moreover, we find that the inequalities are not specific to expressions of the form replaced by any symmetric polynomial with positive coefficients. Moreover, we find that the inequalities are not specific to expressions of the form 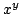 , rather they hold for any function , rather they hold for any function 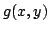 that satisfies some conditions. A simple consequence of this result is a theorem of Hardy, Littlewood and Polya [1]. that satisfies some conditions. A simple consequence of this result is a theorem of Hardy, Littlewood and Polya [1].
[1] G. HARDY, J.E. LITTLEWOOD and G. PÓLYA, Inequalities, Cambridge Univ. Press, 2001.
[2] P. STANICA, Inequalities on linear functions and circular
powers, J. Ineq. in Pure and Applied Math., 3(3) (2002),
Art. 43.
|



