| |
|
|
| |
Volume 4, Issue 4, Article 69 |
|
|
|
|
|
| |
Inequalities for the Transformation Operators and Applications
|
| |
|
Authors: |
Alexander G. Ramm, |
|
| |
|
Keywords:
|
Inequalities, Transformation operators, Inverse scattering |
|
| |
|
Date Received:
|
09/04/03 |
|
| |
|
Date Accepted:
|
07/08/03 |
|
| |
|
Subject Codes: |
34B25,35R30,73D25,81F05,81F15.
|
|
| |
|
Editors: |
Hillel Gauchman, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Inequalities for the transformation operator kernel 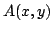 in terms of in terms of 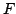 -function are given, and vice versa. These inequalities are applied to inverse scattering on the half-line. Characterization of the scattering data corresponding to the usual scattering class -function are given, and vice versa. These inequalities are applied to inverse scattering on the half-line. Characterization of the scattering data corresponding to the usual scattering class 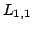 of the potentials, to the class of compactly supported potentials, and to the class of square integrable potentials is given. Invertibility of each of the steps in the inversion procedure is proved. The novel points in this paper include: a) inequalities for the transformation operators in terms of the function of the potentials, to the class of compactly supported potentials, and to the class of square integrable potentials is given. Invertibility of each of the steps in the inversion procedure is proved. The novel points in this paper include: a) inequalities for the transformation operators in terms of the function 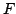 , constructed from the scattering data, b) a considerably shorter way to study the inverse scattering problem on the half-axis and to get necessary and sufficient conditions on the scattering data for the potential to belong to some class of potentials, for example, to the class , constructed from the scattering data, b) a considerably shorter way to study the inverse scattering problem on the half-axis and to get necessary and sufficient conditions on the scattering data for the potential to belong to some class of potentials, for example, to the class 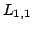 , to itssubclass , to itssubclass 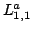 of potentials vanishing for of potentials vanishing for 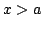 , and for the class of potentials belonging to , and for the class of potentials belonging to 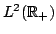 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



