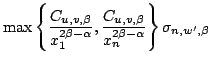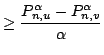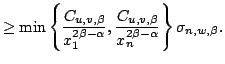JIPAM
| Certain Bounds for the Differences of Means | |||||||
| Authors: | Peng Gao, | ||||||
| Keywords: | Ky Fan's inequality, Levinson's inequality, Generalized weighted power means, Mean value theorem. | ||||||
| Date Received: | 17/08/02 | ||||||
| Date Accepted: | 03/06/03 | ||||||
| Subject Codes: |
26D15,26D20 |
||||||
| Editors: | Kenneth B. Stolarsky, | ||||||
| Abstract: |
Let
Here | ||||||
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=317