JIPAM
| $L^p-$Improving Properties for Measures on $\mathbb{R}^{4}$ Supported on Homogeneous Surfaces in Some Non Elliptic Cases | ||||
| Authors: | E. Ferreyra, T. Godoy, M. Urciuolo, | |||
| Keywords: | Singular Measures, $L^p$-Improving, Convolution Operators. | |||
| Date Received: | 08/01/01 | |||
| Date Accepted: | 05/06/01 | |||
| Subject Codes: |
42B20,42B10. |
|||
| Editors: | Lubos Pick, | |||
| Abstract: |
In this paper we study convolution operators | |||
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=351
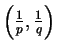 belongs to certain explicitly described trapezoidal region.;
belongs to certain explicitly described trapezoidal region.;