| |
|
|
| |
Volume 2, Issue 3, Article 37 |
|
|
|
|
|
| |
$L^p-$Improving Properties for Measures on $\mathbb{R}^{4}$ Supported on Homogeneous Surfaces in Some Non Elliptic Cases
|
| |
|
Authors: |
E. Ferreyra, T. Godoy, M. Urciuolo, |
|
| |
|
Keywords:
|
Singular Measures, $L^p$-Improving, Convolution Operators. |
|
| |
|
Date Received:
|
08/01/01 |
|
| |
|
Date Accepted:
|
05/06/01 |
|
| |
|
Subject Codes: |
42B20,42B10.
|
|
| |
|
Editors: |
Lubos Pick, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper we study convolution operators 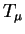 with measures with measures  in in 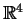 of the form of the form 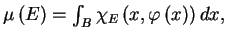 where where 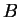 is the unit ball of is the unit ball of 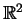 , and , and 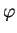 is a homogeneous polynomial function. If is a homogeneous polynomial function. If 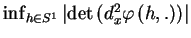 vanishes only on a finite union of lines, we prove that vanishes only on a finite union of lines, we prove that  is bounded from is bounded from 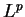 into into 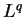 if if 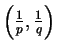 belongs to certain explicitly described trapezoidal region. belongs to certain explicitly described trapezoidal region.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



