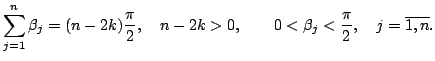JIPAM
| Certain Inequalities Concerning Some Kinds Of Chordal Polygons | |||||||
| Authors: | Mirko Radic, | ||||||
| Keywords: | Inequality, $k$-chordal polygon, $k$-inscribed chordal polygon, index of $k$-inscribed chordal polygon, characteristic of $k$-chordal polygon. | ||||||
| Date Received: | 09/07/03 | ||||||
| Date Accepted: | 25/11/03 | ||||||
| Subject Codes: |
51E12 |
||||||
| Editors: | Jozsef Sandor, | ||||||
| Abstract: |
This paper deals with certain inequalities concerning some kinds of chordal polygons (Definition 1.2). The main part of the article concerns the inequality
| ||||||
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=353