| |
|
|
| |
Volume 6, Issue 2, Article 38 |
|
|
|
|
|
| |
A Refinement of Jensen's Inequality
|
| |
|
Authors: |
Jamal Rooin, |
|
| |
|
Keywords:
|
Product measure, Fubini's Theorem, Jensen's inequality. |
|
| |
|
Date Received:
|
27/08/04 |
|
| |
|
Date Accepted:
|
16/03/05 |
|
| |
|
Subject Codes: |
Primary: 26D15, 28A35.
|
|
| |
|
Editors: |
Charles E. M. Pearce, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
We refine Jensen's inequality as where 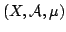 and and 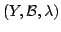 are two probability measure spaces, are two probability measure spaces, 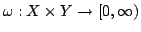 is a weight function on is a weight function on 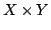 , , 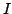 is an interval of the real line, is an interval of the real line, 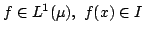 for all for all 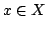 and and 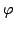 is a real-valued convex function on is a real-valued convex function on 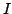 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|