| |
|
|
| |
Volume 6, Issue 3, Article 77 |
|
|
|
|
|
| |
A General Optimal Inequality for Arbitrary Riemannian Submanifolds
|
| |
|
Authors: |
Bang-Yen Chen, |
|
| |
|
Keywords:
|
$delta$-invariants, Inequality, Riemannian submanifold, Squared mean curvature, Sectional curvature. |
|
| |
|
Date Received:
|
22/03/05 |
|
| |
|
Date Accepted:
|
28/07/05 |
|
| |
|
Subject Codes: |
53C40, 53C42, 53B25
|
|
| |
|
Editors: |
Wing-Sum Cheung, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
One of the most fundamental problems in submanifold theory is to establish simple relationships between intrinsic and extrinsic invariants of the submanifolds (cf. [6]). A general optimal inequality for submanifolds in Riemannian manifolds of constant sectional curvature was obtained in an earlier article [5]. In this article we extend this inequality to a general optimal inequality for arbitrary Riemannian submanifolds in an arbitrary Riemannian manifold. This new inequality involves only the 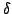 -invariants, the squared mean curvature of the submanifolds and the maximum sectional curvature of the ambient manifold. Several applications of this new general inequality are also presented. -invariants, the squared mean curvature of the submanifolds and the maximum sectional curvature of the ambient manifold. Several applications of this new general inequality are also presented.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



