Primary 47B47, 47A30, 47B20; Secondary 4

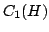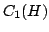The general problem in this paper is minimizing the -norm of suitable affine mappings from to , using convex and differential analysis (Gâteaux derivative) as well as input from operator theory. The mappings considered generalize the so-called elementary operators and in particular the generalized derivations, which are of great interest by themselves. The main results obtained characterize global minima in terms of (Banach space) orthogonality, and constitute an interesting combination of infinite-dimensional differential analysis, convex analysis, operator theory and duality.;