|
JIPAM
| On L'Hospital-Type Rules for Monotonicity |
|
|
|
|
| |
| |
Authors: |
Iosif Pinelis, |
|
| |
Keywords:
|
L'Hospital-type rules, Monotonicity, Borwein-Borwein-Rooin ratio, Becker-Stark inequalities, Anderson-Vamanamurthy-Vuorinen inequalities, log-concavity, Maclaurin series, Hyperbolic geometry, Right-angled triangles. |
|
| |
Date Received:
|
18/05/05 |
|
| |
Date Accepted:
|
14/11/05 |
|
| |
Subject Codes: |
26A48, 26A51, 26A82, 26D10, 50C10, 53A35
|
|
| |
Editors: |
Jonathan Borwein, |
|
| |
|
|
|
|
| |
Abstract: |
Elsewhere we developed rules for the monotonicity pattern of the ratio 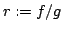 of two differentiable functions on an interval of two differentiable functions on an interval 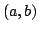 based on the monotonicity pattern of the ratio based on the monotonicity pattern of the ratio 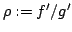 of the derivatives. Those rules are applicable even more broadly than l'Hospital's rules for limits, since in general we do not require that both of the derivatives. Those rules are applicable even more broadly than l'Hospital's rules for limits, since in general we do not require that both 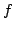 and and 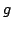 , or either of them, tend to 0 or , or either of them, tend to 0 or 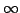 at an endpoint or any other point of at an endpoint or any other point of 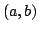 . Here new insight into the nature of the rules for monotonicity is provided by a key lemma, which implies that, if . Here new insight into the nature of the rules for monotonicity is provided by a key lemma, which implies that, if 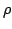 is monotonic, then is monotonic, then 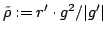 is so; hence, is so; hence, 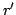 changes sign at most once. Based on the key lemma, a number of new rules are given. One of them is as follows: Suppose that changes sign at most once. Based on the key lemma, a number of new rules are given. One of them is as follows: Suppose that 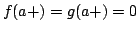 ; suppose also that ; suppose also that 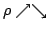 on on 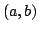 - that is, for some - that is, for some 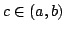 , , 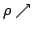 ( (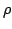 is increasing) on is increasing) on 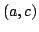 and and 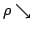 on on 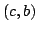 . Then . Then 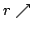 or or  on on 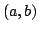 . Various applications and illustrations are given. ; . Various applications and illustrations are given. ;
|
This article was printed from JIPAM
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=657
|