| |
|
|
| |
Volume 7, Issue 2, Article 53 |
|
|
|
|
|
| |
On a Generalized $n-$inner Product and the Corresponding Cauchy-Schwarz Inequality
|
| |
|
Authors: |
Kostadin Trencevski, Risto Malcevski, |
|
| |
|
Keywords:
|
Cauchy-Schwarz inequality, $n$-inner product, $n$-norm. |
|
| |
|
Date Received:
|
22/11/04 |
|
| |
|
Date Accepted:
|
27/02/06 |
|
| |
|
Subject Codes: |
46C05, 26D20.
|
|
| |
|
Editors: |
Constantin P. Niculescu, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper is defined an 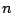 -inner product of type -inner product of type 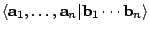 where where 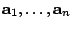 , ,  are vectors from a vector space are vectors from a vector space  . This definition generalizes the definition of Misiak of . This definition generalizes the definition of Misiak of 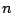 -inner product [2], such that in special case if we consider only such pairs of sets -inner product [2], such that in special case if we consider only such pairs of sets 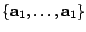 and and 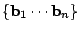 which differ for at most one vector, we obtain the definition of Misiak. The Cauchy-Schwarz inequality for this general type of which differ for at most one vector, we obtain the definition of Misiak. The Cauchy-Schwarz inequality for this general type of 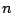 -inner product is proved and some applications are given. -inner product is proved and some applications are given.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



