JIPAM
| On Minkowski and Hardy Integral Inequalities | ||||
| Authors: | Lazhar Bougoffa, | |||
| Keywords: | Minkowski's inequality, Hardy's inequality. | |||
| Date Received: | 30/11/05 | |||
| Date Accepted: | 15/01/06 | |||
| Subject Codes: |
26D15. |
|||
| Editors: | Bicheng Yang, | |||
| Abstract: |
The reverse Minkowski's integral inequality: 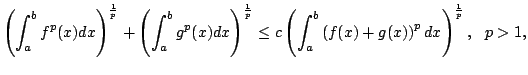 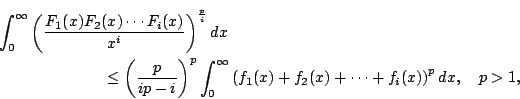 where 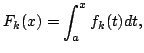 where where | |||
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=677