| |
|
|
| |
Volume 7, Issue 3, Article 117 |
|
|
|
|
|
| |
Fekete-Szegö Functional for some Subclass of Non-Bazilevic Functions
|
| |
|
Authors: |
T.N. Shanmugam, M.P. Jeyaraman, S. Sivasubramanian, |
|
| |
|
Keywords:
|
Analytic functions, Starlike functions, Subordination, Coefficient problem, Fekete-Szegö inequality. |
|
| |
|
Date Received:
|
18/11/05 |
|
| |
|
Date Accepted:
|
24/03/06 |
|
| |
|
Subject Codes: |
Primary 30C45.
|
|
| |
|
Editors: |
Alexandru Lupas (1942-2007), |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this present investigation, the authors obtain a sharp Fekete-Szegö's inequality for certain normalized analytic functions 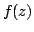 defined on the open unit disk for which defined on the open unit disk for which 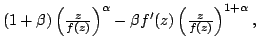 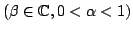 lies in a region starlike with respect to lies in a region starlike with respect to 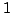 and is symmetric with respect to the real axis. Also, certain applications of our results for a class of functions defined by convolution are given. As a special case of this result, Fekete-Szegö's inequality for a class of functions defined through fractional derivatives is also obtained. and is symmetric with respect to the real axis. Also, certain applications of our results for a class of functions defined by convolution are given. As a special case of this result, Fekete-Szegö's inequality for a class of functions defined through fractional derivatives is also obtained.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



