| |
|
|
| |
Volume 7, Issue 4, Article 145 |
|
|
|
|
|
| |
A Coefficient Inequality For Certain Classes Of Analytic Functions Of Complex Order
|
| |
|
Authors: |
K. Suchithra, B. Adolf Stephen, S. Sivasubramanian, |
|
| |
|
Keywords:
|
Starlike functions of complex order, Convex functions of complex order, Subordination, Fekete-Szegö inequality |
|
| |
|
Date Received:
|
06/02/06 |
|
| |
|
Date Accepted:
|
25/08/06 |
|
| |
|
Subject Codes: |
Primary 30C45.
|
|
| |
|
Editors: |
Gabriela Kohr, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In the present investigation, we obtain the Fekete-Szegö inequality for a certain normalized analytic function 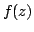 defined on the open unit disk for which defined on the open unit disk for which ![$ 1 + frac{1}{b}left[frac{zf^prime(z) + alpha z^2f^{primeprime}(z)}{f(z)} - 1right]$](images/032_06_JIPAM/img2.gif) ( ( 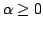 and and 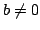 , a complex number) lies in a region starlike with respect to 1 and symmetric with respect to real axis. Also certain application of the main result for a class of functions of complex order defined by convolution is given. The motivation of this paper is to give a generalization of the Fekete-Szegö inequalities for subclasses of starlike functions of complex order. , a complex number) lies in a region starlike with respect to 1 and symmetric with respect to real axis. Also certain application of the main result for a class of functions of complex order defined by convolution is given. The motivation of this paper is to give a generalization of the Fekete-Szegö inequalities for subclasses of starlike functions of complex order.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



