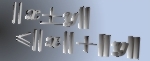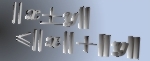| |
|
|
| |
Volume 7, Issue 5, Article 166 |
|
|
|
|
|
| |
Estimating the Sequence of Real Binomial Coefficients
|
| |
|
Authors: |
Vito Lampret, |
|
| |
|
Keywords:
|
Approximation, Binomial, Coefficient, Convergence, Estimate, Error, DeMoivre-Laplace, Euler-Maclaurin, Remainder, Sequence. |
|
| |
|
Date Received:
|
02/03/06 |
|
| |
|
Date Accepted:
|
17/03/06 |
|
| |
|
Subject Codes: |
05A10, 26D07, 26D15, 33F05, 40A05, 40A25
|
|
| |
|
Editors: |
Jozsef Sandor, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
The sequence 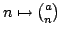 of real binomial coefficients is studied in two main cases: of real binomial coefficients is studied in two main cases: 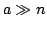 and and 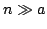 . In the first case a uniform approximation with high accuracy is obtained, in contrast to DeMoivre-Laplace approximation, which has essentially local character and is good only for . In the first case a uniform approximation with high accuracy is obtained, in contrast to DeMoivre-Laplace approximation, which has essentially local character and is good only for 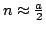 . In the second case, for every . In the second case, for every 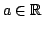  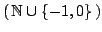 , the functions , the functions 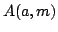 and and 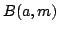 are determined, such that are determined, such that 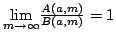 , and , and for integers 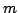 and and 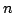 , obeying , obeying 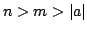 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|