| |
|
|
| |
Volume 7, Issue 5, Article 174 |
|
|
|
|
|
| |
A New Obstruction to Minimal Isometric Immersions into a Real Space Form
|
| |
|
Authors: |
Teodor Oprea, |
|
| |
|
Keywords:
|
Constrained maximum, Chen's inequality, Minimal submanifolds. |
|
| |
|
Date Received:
|
29/11/05 |
|
| |
|
Date Accepted:
|
23/11/06 |
|
| |
|
Subject Codes: |
53C21, 53C24, 49K35.
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In the theory of minimal submanifolds, the following problem is fundamental: when does a given Riemannian manifold admit (or does not admit) a minimal isometric immersion into an Euclidean space of arbitrary dimension? S.S. Chern, in his monograph [6] Minimal submanifolds in a Riemannian manifold, remarked that the result of Takahashi (the Ricci tensor of a minimal submanifold into a Euclidean space is negative semidefinite) was the only known Riemannian obstruction to minimal isometric immersions in Euclidean spaces. A second obstruction was obtained by B.Y. Chen as an immediate application of his fundamental inequality [1]: the scalar curvature and the sectional curvature of a minimal submanifold into a Euclidean space satisfies the inequality  We find a new relation between the Chen invariant, the dimension of the submanifold, the length of the mean curvature vector field and a deviation parameter. This result implies a new obstruction: the sectional curvature of a minimal submanifold into a Euclidean space also satisfies the inequality We find a new relation between the Chen invariant, the dimension of the submanifold, the length of the mean curvature vector field and a deviation parameter. This result implies a new obstruction: the sectional curvature of a minimal submanifold into a Euclidean space also satisfies the inequality 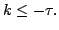
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



