JIPAM

Local Estimates for Jacobi Polynomials  
 
  Authors: Michael Felten,  
  Keywords: Jacobi polynomials, Jacobi weights, Local estimates.  
  Date Received: 12/10/06  
  Date Accepted: 02/01/07  
  Subject Codes:

33C45, 42C05.

  
  Editors: Alexandru Lupas (1942-2007),  
 
  Abstract:

It is shown that if 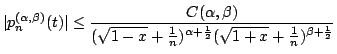$ $ alpha,$ beta$ geq-{$ frac{1}{2}}$, then the orthonormal Jacobi polynomials $ p_n^{($ alpha,$ beta)}$ fulfill the local estimate

$ displaystyle $ vert p_n^{($ alpha,$ beta)}(t)$ vert $ leq {$ frac{C($ alpha,$ beta)}{(... ...}})^{$ alpha+{$ frac{1}{2}}} ($ sqrt{1+x}+{$ frac{1}{n}})^{$ beta+{$ frac{1}{2} }}}} $
for all $ t$ in U_n(x)$ and each $ x$ in[-1,1]$, where $ U_n(x)$ are subintervals of $ [-1,1]$ defined by $ U_n(x)=[x-{$ frac{$ varphi_n(x)}{n}},x+{ $ frac{$ varphi_n(x)}{n}}]$ cap[-1,1]$ for $ n$ in$ mathbb{N}$ and $ x$ in[-1,1]$ with $ $ varphi_n(x)=$ sqrt{1-x^2}+{$ frac{1}{n}}$. Applications of the local estimate are given at the end of the paper. ;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=816