| |
|
|
| |
Volume 8, Issue 1, Article 4 |
|
|
|
|
|
| |
On an Opial Inequality with a Boundary Condition
|
| |
|
Authors: |
Man Kam Kwong, |
|
| |
|
Keywords:
|
Opial inequality, Integral condition, Calculus of variation. |
|
| |
|
Date Received:
|
01/11/06 |
|
| |
|
Date Accepted:
|
08/03/07 |
|
| |
|
Subject Codes: |
26D10, 26D15.
|
|
| |
|
Editors: |
Don B. Hinton, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
R.C. Brown conjectured (in 2001) that the Opial-type inequality holds for all absolutely continuous functions ![$ y:[0,1]$ rightarrow $ mathbb{R} $](images/279_06_JIPAM/img2.gif) such that such that 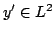 and and  . This was subsequently proved by Denzler [3]. An alternative proof was given by Brown and Plum [2]. Here we give a shorter proof. . This was subsequently proved by Denzler [3]. An alternative proof was given by Brown and Plum [2]. Here we give a shorter proof.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



