| |
|
|
| |
Volume 8, Issue 1, Article 11 |
|
|
|
|
|
| |
Redheffer Type Inequality for Bessel Functions
|
| |
|
Authors: |
Árpád Baricz, |
|
| |
|
Keywords:
|
Bessel functions, Modified Bessel functions, Redheffer's inequality. |
|
| |
|
Date Received:
|
23/08/06 |
|
| |
|
Date Accepted:
|
09/02/07 |
|
| |
|
Subject Codes: |
33C10, 26D05.
|
|
| |
|
Editors: |
Feng Qi, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this short note, by using mathematical induction and infinite product representations of the functions ![$ $ mathcal{J}_p:$ mathbb{R} $ rightarrow(-$ infty,1]$](images/220_06_JIPAM/img1.gif) and and 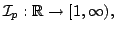 defined by defined by 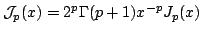 and 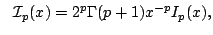 an extension of Redheffer's inequality for the function 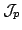 and a Redheffer-type inequality for the function and a Redheffer-type inequality for the function 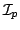 are established. Here are established. Here 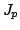 and and 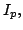 denotes the Bessel function and modified Bessel function, while denotes the Bessel function and modified Bessel function, while 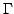 stands for the Euler gamma function. At the end of this work a lower bound for the stands for the Euler gamma function. At the end of this work a lower bound for the 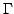 function is deduced, using Euler's infinite product formula. Our main motivation to write this note is the publication of C.P. Chen, J.W. Zhao and F. Qi [2], which we wish to complement. function is deduced, using Euler's infinite product formula. Our main motivation to write this note is the publication of C.P. Chen, J.W. Zhao and F. Qi [2], which we wish to complement.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



