| |
|
Abstract: |
Assuming that a ``derivative'' ratio 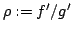 of the ratio of the ratio 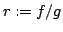 of differentiable functions of differentiable functions  and and 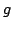 is strictly monotonic (that is, is strictly monotonic (that is, 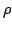 is increasing or decreasing), it was shown in previous papers that then is increasing or decreasing), it was shown in previous papers that then 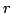 can switch at most once, from decrease to increase or vice versa. In the present paper, it is shown that, if can switch at most once, from decrease to increase or vice versa. In the present paper, it is shown that, if 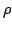 is non-strictly monotonic (that is, non-increasing or non-decreasing), then is non-strictly monotonic (that is, non-increasing or non-decreasing), then 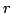 can have at most one maximal interval of constancy (m.i.c.); on the other hand, any one m.i.c. of a given derivative ratio can have at most one maximal interval of constancy (m.i.c.); on the other hand, any one m.i.c. of a given derivative ratio 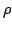 is the m.i.c. of an appropriately constructed original ratio is the m.i.c. of an appropriately constructed original ratio 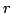 . .
|



