| |
|
|
| |
Volume 8, Issue 2, Article 51 |
|
|
|
|
|
| |
$S$-Geometric Convexity of a Function Involving Maclaurin's Elementary Symmetric Mean
|
| |
|
Authors: |
Xiao-Ming Zhang, |
|
| |
|
Keywords:
|
Geometrically convex function, $S$-geometrically convex function, Inequality, Maclaurin-Inequality, Logarithm majorization. |
|
| |
|
Date Received:
|
23/02/07 |
|
| |
|
Date Accepted:
|
27/04/07 |
|
| |
|
Subject Codes: |
Primary 26D15.
|
|
| |
|
Editors: |
Peter S. Bullen, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 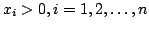 , , 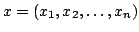 , the , the  th elementary symmetric function of th elementary symmetric function of 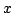 is defined as is defined as 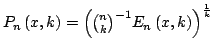 , and the function , and the function 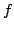 is defined as is defined as  . The paper proves that . The paper proves that 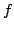 is a S-geometrically convex function. The result generalizes the well-known Maclaurin-Inequality. is a S-geometrically convex function. The result generalizes the well-known Maclaurin-Inequality.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



