| |
|
|
| |
Volume 8, Issue 2, Article 36 |
|
|
|
|
|
| |
Dirichlet Green Functions for Parabolic Operators with Singular Lower-Order Terms
|
| |
|
Authors: |
Lotfi Riahi, |
|
| |
|
Keywords:
|
Green function, Parabolic operator, Initial-Dirichlet problem, Boundary behavior, Singular potential, Singular drift term, Radon measure, Schrödinger heat kernel, Parabolic Kato class. |
|
| |
|
Date Received:
|
15/03/06 |
|
| |
|
Date Accepted:
|
10/04/07 |
|
| |
|
Subject Codes: |
34B27, 35K10.
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
We prove the existence and uniqueness of a continuous Green function for the parabolic operator 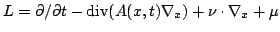 with the initial Dirichlet boundary condition on a with the initial Dirichlet boundary condition on a 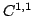 -cylindrical domain -cylindrical domain 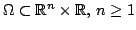 , satisfying lower and upper estimates, where , satisfying lower and upper estimates, where 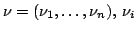 and and 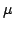 are in general classes of signed Radon measures covering the well known parabolic Kato classes. are in general classes of signed Radon measures covering the well known parabolic Kato classes.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|