| |
|
|
| |
Volume 8, Issue 3, Article 89 |
|
|
|
|
|
| |
Hyers-Ulam-Rassias Stability of the $K$-Quadratic Functional Equation
|
| |
|
Authors: |
Mohamed Ait Sibaha, Belaid Bouikhalene, Elhoucien Elqorachi, |
|
| |
|
Keywords:
|
Group, Additive equation, Quadratic equation, Hyers-Ulam-Rassias stability. |
|
| |
|
Date Received:
|
26/01/07 |
|
| |
|
Date Accepted:
|
08/06/07 |
|
| |
|
Subject Codes: |
39B82, 39B52, 39B32.
|
|
| |
|
Editors: |
Kazimierz Nikodem, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper we obtain the Hyers-Ulam-Rassias stability for the functional equation where  is a finite cyclic transformation group of the abelian group is a finite cyclic transformation group of the abelian group 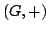 , acting by automorphisms of , acting by automorphisms of  . As a consequence we can derive the Hyers-Ulam-Rassias stability of the quadratic and the additive functional equations. . As a consequence we can derive the Hyers-Ulam-Rassias stability of the quadratic and the additive functional equations.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



