| |
|
|
| |
Volume 9, Issue 2, Article 33 |
|
|
|
|
|
| |
Asymptotic Behavior for Discretizations of a Semilinear Parabolic Equation with a Nonlinear Boundary Condition
|
| |
|
Authors: |
Nabongo Diabate, Théodore K. Boni, |
|
| |
|
Keywords:
|
Semidiscretizations, Semilinear parabolic equation, Asymptotic behavior, Convergence. |
|
| |
|
Date Received:
|
16/10/07 |
|
| |
|
Date Accepted:
|
17/03/08 |
|
| |
|
Subject Codes: |
35B40, 35B50, 35K60, 65M06.
|
|
| |
|
Editors: |
Catherine Bandle, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
This paper concerns the study of the numerical approximation for the following initial-boundary value problem: ![$displaystyle left{ begin{array}{ll} hbox{$u_t=u_{xx} -avert uvert^{p-1}u... ... [5pt] hbox{$u(x,0)=u_{0}(x)>0,quad 0leq x leq 1$,} & end{array} right.$](images/314_07_JIPAM/img1.gif) | (P) | where  , , 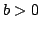 and and 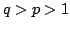 . We show that the solution of a semidiscrete form of (P) goes to zero as . We show that the solution of a semidiscrete form of (P) goes to zero as  goes to infinity and give its asymptotic behavior. Using some nonstandard schemes, we also prove some estimates of solutions for discrete forms of (P). Finally, we give some numerical experiments to illustrate our analysis. goes to infinity and give its asymptotic behavior. Using some nonstandard schemes, we also prove some estimates of solutions for discrete forms of (P). Finally, we give some numerical experiments to illustrate our analysis.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



