| |
|
|
| |
Volume 6, Issue 4, Article 110 |
|
|
|
|
|
| |
Young's Inequality In Compact Operators - The Case Of Equality
|
| |
|
Authors: |
Renying Zeng, |
|
| |
|
Keywords:
|
Young's Inequality, compact normal operator, Hilbert space. |
|
| |
|
Date Received:
|
24/08/05 |
|
| |
|
Date Accepted:
|
22/09/05 |
|
| |
|
Subject Codes: |
47A63, 15A60.
|
|
| |
|
Editors: |
Fuzhen Zhang, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
If  and and 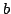 are compact operators acting on a complex separable Hilbert space, and if are compact operators acting on a complex separable Hilbert space, and if 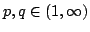 satisfy satisfy 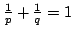 , then there exists a partial isometry , then there exists a partial isometry 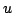 such that the initial space of such that the initial space of 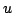 is is 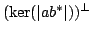 and and
Furthermore, if 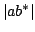 is injective, then the operator is injective, then the operator 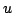 in the inequality above can be taken as a unitary. In this paper, we discuss the case of equality of this Young's inequality, and obtain a characterization for compact normal operators. in the inequality above can be taken as a unitary. In this paper, we discuss the case of equality of this Young's inequality, and obtain a characterization for compact normal operators.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



