| |
|
Abstract: |
Let 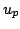 denote the normalized, generalized Bessel function of order denote the normalized, generalized Bessel function of order 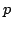 which depends on two parameters which depends on two parameters 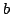 and and 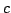 and let and let  , , 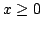 . It is proven that under some conditions imposed on . It is proven that under some conditions imposed on 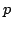 , , 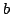 , and , and 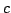 the Askey inequality holds true for the function the Askey inequality holds true for the function 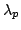 , i.e., that , i.e., that  , where , where 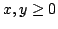 and and 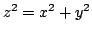 . The lower and upper bounds for the function . The lower and upper bounds for the function 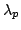 are also established. are also established.
|



