| |
|
|
| |
Volume 7, Issue 1, Article 7 |
|
|
|
|
|
| |
Approximation of $\pi(x)$ by $\Psi(x)$
|
| |
|
Authors: |
Mehdi Hassani, |
|
| |
|
Keywords:
|
Primes, Harmonic series, Gamma function, Digamma function. |
|
| |
|
Date Received:
|
07/03/05 |
|
| |
|
Date Accepted:
|
25/08/05 |
|
| |
|
Subject Codes: |
11A41, 26D15, 33B15.
|
|
| |
|
Editors: |
Jozsef Sandor, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper we find some lower and upper bounds of the form 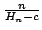 for the function for the function  , in which , in which  . Then, we consider . Then, we consider 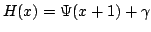 as generalization of as generalization of  , such that , such that 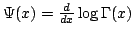 and and 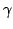 is Euler constant; this extension has been introduced for the first time by J. Sándor and it helps us to find some lower and upper bounds of the form is Euler constant; this extension has been introduced for the first time by J. Sándor and it helps us to find some lower and upper bounds of the form 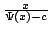 for the function for the function 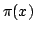 and using these bounds, we show that and using these bounds, we show that 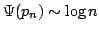 , when , when 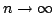 is equivalent with the Prime Number Theorem. is equivalent with the Prime Number Theorem.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



