| |
|
|
| |
Volume 7, Issue 2, Article 50 |
|
|
|
|
|
| |
Coefficient Inequality For A Function Whose Derivative Has A Positive Real Part
|
| |
|
Authors: |
Aini Janteng, Suzeini Abdul Halim, Maslina Darus, |
|
| |
|
Keywords:
|
Fekete-Szegö functional, Hankel determinant, Convex and starlike functions, Positive real functions. |
|
| |
|
Date Received:
|
07/03/05 |
|
| |
|
Date Accepted:
|
09/03/06 |
|
| |
|
Subject Codes: |
Primary 30C45.
|
|
| |
|
Editors: |
Anthony Sofo, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 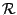 denote the subclass of normalised analytic univalent functions denote the subclass of normalised analytic univalent functions 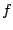 defined by defined by 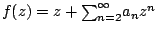 and satisfy and satisfy
where 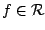 , we give sharp upper bound for , we give sharp upper bound for 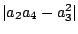 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|