| |
|
|
| |
Volume 7, Issue 3, Article 99 |
|
|
|
|
|
| |
A Note on Multiplicatively $e$-perfect Numbers
|
| |
|
Authors: |
Le Anh Vinh, Dang Phuong Dung, |
|
| |
|
Keywords:
|
Perfect number, Exponential divisor, Multiplicatively perfect, Sum of divisors, Number of divisors. |
|
| |
|
Date Received:
|
17/10/05 |
|
| |
|
Date Accepted:
|
26/10/05 |
|
| |
|
Subject Codes: |
11A25, 11A99.
|
|
| |
|
Editors: |
Jozsef Sandor, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 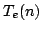 denote the product of all exponential divisors of denote the product of all exponential divisors of 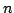 . An integer . An integer 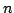 is called multiplicatively is called multiplicatively 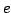 -perfect if -perfect if 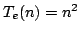 and multiplicatively and multiplicatively 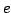 -superperfect if -superperfect if 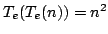 . In this note, we give an alternative proof for characterization of multiplicatively . In this note, we give an alternative proof for characterization of multiplicatively 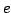 -perfect and multiplicatively -perfect and multiplicatively 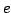 -superperfect numbers. -superperfect numbers.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|