| |
|
|
| |
Volume 7, Issue 3, Article 114 |
|
|
|
|
|
| |
Generalized Nonlinear Mixed Quasi-Variational Inequalities Involving Maximal $\eta$-Monotone Mappings
|
| |
|
Authors: |
Mao-Ming Jin, |
|
| |
|
Keywords:
|
Mixed quasi-variational inequality, Maximal $eta$-monotone mapping, Resolvent operator, Convergence, stability. |
|
| |
|
Date Received:
|
27/07/04 |
|
| |
|
Date Accepted:
|
09/05/06 |
|
| |
|
Subject Codes: |
49J40; 47H10.
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, we introduce and study a new class of generalized nonlinear mixed quasi-variational inequalities involving maximal 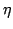 -monotone mapping. Using the resolvent operator technique for maximal -monotone mapping. Using the resolvent operator technique for maximal 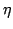 -monotone mapping, we prove the existence of solution for this kind of generalized nonlinear multi-valued mixed quasi-variational inequalities without compactness and the convergence of iterative sequences generated by the new algorithm. We also discuss the convergence and stability of the iterative sequence generated by the perturbed iterative algorithm for solving a class of generalized nonlinear mixed quasi-variational inequalities. -monotone mapping, we prove the existence of solution for this kind of generalized nonlinear multi-valued mixed quasi-variational inequalities without compactness and the convergence of iterative sequences generated by the new algorithm. We also discuss the convergence and stability of the iterative sequence generated by the perturbed iterative algorithm for solving a class of generalized nonlinear mixed quasi-variational inequalities.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



