| |
|
|
| |
Volume 7, Issue 5, Article 163 |
|
|
|
|
|
| |
Direct Approximation Theorems for Discrete Type Operators
|
| |
|
Authors: |
Zoltán Finta, |
|
| |
|
Keywords:
|
Direct approximation theorem, $K-$functional, Ditzian-Totik modulus of smoothness. |
|
| |
|
Date Received:
|
16/07/06 |
|
| |
|
Date Accepted:
|
10/10/06 |
|
| |
|
Subject Codes: |
41A36, 41A25.
|
|
| |
|
Editors: |
Zeev Ditzian, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In the present paper we prove direct approximation theorems for discrete type operators 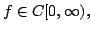 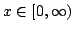 using a modified using a modified 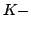 functional. As applications we give direct theorems for Baskakov type operators, Szász-Mirakjan type operators and Lupas operator. functional. As applications we give direct theorems for Baskakov type operators, Szász-Mirakjan type operators and Lupas operator.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|